For snart 60 år siden dokumenterte den amerikanske psykologen og statistikeren Jacob Cohen (1962) at mange studier i psykologisk forskning ble gjennomført med lav statistisk styrke. Dette er et problem fordi den statistiske styrken til en studie sier noe om sannsynligheten for at vi avdekker en effekt, dersom det finnes en effekt å avdekke.

Mindre kjent, eller i hvert fall inntil nylig mindre omtalt, er det faktumet at lav statistisk styrke også medfører at vi «finner» effekter eller fenomener som ikke er der. Dette medfører trolig at nokså mange forskningsresultater rett og slett er usanne. Hvordan dette kan ha seg skal jeg komme tilbake til, men først skal vi gjøre forsøk på å forstå ideen om statistisk styrke, slik den ofte fremstilles, uten å gjøre det altfor teknisk.

Et eksempel på statistisk styrke

Tenk deg at noen kloke psykologer, basert på år med solid grunnforskning, har utarbeidet en ny type terapi for en eller annen lidelse. På grunnlag av både teori og forskning mener de å kunne argumentere for at den nye terapien vil være mer effektiv enn eksisterende behandling. For å undersøke om de har rett trekker vi ut et håndterbart utvalg deltakere fra den relevante populasjonen (alle med den aktuelle lidelsen), og fordeler dem tilfeldig til en intervensjonsgruppe som får den nye behandlingen, og en kontrollgruppe som får den vanlige behandlingen. Når behandlingene er ferdig gjennomført, måler vi et relevant, forhåndsdefinert utfall, f.eks. symptomtrykket hos deltakerne i hver gruppe.

Et avgjørende ledd i denne prosessen er den statistiske analysen av gruppeforskjellene – den statistiske hypotesetestingen. Den er avgjørende av mange grunner, men kanskje først og fremst på grunn av tilfeldig variasjon: En mengde ukjente faktorer, ikke bare terapiene, vil påvirke det vi måler. Symptomtrykket vil variere i utvalget så vel som innad i begge gruppene, både før og etter behandlingene. Utvalget vil ikke være helt likt populasjonen, og gruppene i utvalget vil ikke være helt like hverandre. I tillegg vil målingene våre sjelden være helt presise, altså nok en faktor som bidrar til variasjon. Fenomenet vi er ute etter å avdekke, denne mulige forskjellen mellom gruppene, er liksom pakket inn i masse støy. Den statistiske hypotesetestingen, brukt riktig, er et verktøy for å se forbi denne støyen og hjelpe oss til å se om det virkelig er noe nyttig der inne.

La oss først anta at psykologene bak den nye terapien har rett, altså at det i virkeligheten ville være slik at dersom vi behandlet hele populasjonen (alle de som har lidelsen) med den nye terapien, så ville det gjennomsnittlige symptomtrykket reduseres mer enn ved den gamle terapien. Hva må til for at vi skal finne igjen denne virkeligheten i utvalgsstudien vår? Med andre ord: Hva skal til for at vi får en statistisk signifikant forskjell mellom de to gruppene og slik kunne avvise den usanne nullhypotesen om at gruppene er like?¹

Svaret på dette spørsmålet handler mye om statistisk styrke. Og svaret er, noe upresist og ufullstendig, at det avhenger av hvor stor den sanne forskjellen i populasjonen er, og samtidig av hvor stort utvalget vårt er. Hvis den sanne avstanden mellom de to terapiene er et halvt standardavvik², hvilket i denne sammenhengen kan regnes som en middels stor forskjell (eller effektstørrelse), og vi har et utvalg på til sammen hundre deltakere (med 50 i hver gruppe), så vil vår statistiske hypotesetest avdekke en forskjell mellom gruppene i om lag 71 % av tilfellene. Dette er litt mindre enn det konvensjonelle, ønskede minimum, som er 80 %. Med 30 deltakere i hver gruppe faller styrken til 49 %.

I Cohens undersøkelse, som omfattet studier i sosialpsykologi og abnormalpsykologi, lå den gjennomsnittlige sannsynligheten for å finne en antatt mellomstor effekt på rundt 50 %. Det er et uakseptabelt lavt styrkenivå. Gjennomfører vi mange studier under de samme forutsetningene, vil halvparten finne effekten og halvparten ikke, selv om det altså er en effekt å finne. En enkel opptelling av signifikante effekter fra slike studier vil lett føre til at vi feilaktig konkluderer med at effekten i beste fall er usikker. Slike tilstander kan også føre til at forskere kaster bort tid og ressurser på å spekulere seg fram til og debattere ulike forklaringer på hvorfor studiene får «forskjellig» resultat.³

Spuriøse effekter

Lav statistisk styrke gjør altså at vi løper en betydelig risiko for ikke å finne reelle og nyttige effekter i forskningsstudiene våre, til tross for at de kanskje egentlig finnes i de populasjonene vi studerer. Denne typen feil kalles gjerne for Type 2-feil. Dette problemet er velkjent, og statistisk styrke forklares på omtrent samme måte som jeg gjør her og vektlegger akkurat dette problemet både i lærebøker og andre steder. (Se Kraemer, 2013 for en litt mer formell, langt mer presis og grundig, men stadig nokså lesbar gjennomgang, eller Cohen, 1992 for en gjennomgang som så å si er helt matematikkfri.)

Et minst like interessant og alvorlig problem er det faktum at lav statistisk styrke også kan føre til at vi «finner» effekter og fenomener som ikke er der. At det er slik, er mindre opplagt og tradisjonelt ikke så ofte omtalt. Så hvordan kan det ha seg?

La oss nå anta at psykologene våre tar feil, altså at det i virkeligheten var slik at dersom vi hadde behandlet hele populasjonen (alle de som har lidelsen) med den nye terapien, så ville det gjennomsnittlige symptomtrykket forbli det samme som ved den gamle terapien. Det er altså i virkeligheten ingen forskjell mellom gruppene. I dette tilfellet er sannsynligheten for at vår statistiske hypotesetest feilaktig indikerer at der er en forskjell, at vi får en spuriøs effekt og begår det som kalles en Type 1-feil, nokså liten. Denne sannsynligheten bestemmes av det såkalte alfanivået, som forskeren selv velger som en parameter for testen sin. Alfanivået settes vanligvis, per konvensjon, til 0,05 i psykologisk forskning.

Hvis vi oppsummerer så langt, så kan vi si at når det faktisk er en reell effekt å oppdage, så er sannsynligheten for å avdekke den via en statistisk test bestemt av den statistiske styrken. På den annen side, når det, i et gitt tilfelle, faktisk ikke er noen effekt å finne, så er sannsynligheten for at vi feilaktig «avdekker» den bestemt av alfanivået, som vi vanligvis setter til 0,05.

Det springende punktet, og kjernen i problemet her, er at ingen forskere opererer i miljøer hvor alle effekter alltid er virkelige eller alle effekter alltid ikke er virkelige. De jobber i miljøer hvor noen effekter er reelle og noen effekter ikke er reelle, og hvor de ikke på forhånd vet hva som er hva. I slike miljøer er sannsynligheten over tid for at en statistisk test gir oss en spuriøs effekt bestemt ikke av alfanivået alene, men også av (det ukjente) forholdet mellom mengden av virkelige effekter og ikke virkelige effekter, og, som nevnt, den statiske styrken.

Denne sannsynligheten ble av den amerikanske psykiateren John E. Overall (som døde tidligere i år) kalt for den betingede alfasannsynligheten (Overall, 1969). Den kan uttrykkes slik:

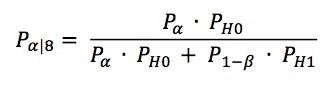
P_α er alfanivået (vanligvis 0,05), P_H0 er (den ukjente) sannsynligheten for at der ikke er noen reell effekt å finne, P_1-β er den statistiske styrken og P_H1 er (den ukjente) sannsynligheten for at der er en reell effekt å finne.

Hvis vi vender tilbake til eksempelet vårt og antar at sannsynligheten for at den nye terapien er bedre enn den eksisterende, altså at der er en reell effekt å finne, er omtrent 10 %⁴, at den statistiske styrken i studien vår er på det ideelle minimum av 80 % og at vi opererer med det konvensjonelle alfanivået på 0,05, så får vi en betinget alfasannsynlighet på

Under disse forholdene får vi altså at sannsynligheten for at en statistisk signifikant hypotesetest egentlig er en spuriøs effekt er merkbart høyere enn det valgte alfanivået. Og hvis den statistiske styrken er mindre enn det ideelle minimum, hvis vi f.eks. nøyer oss med 30 deltakere i hver gruppe (en styrke på 49% – omtrent der Cohen fant at den gjennomsnittlige psykologistudien lå i 1962), så får vi en betinget alfasannsynlighet på

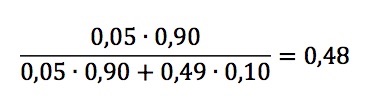
og en situasjon hvor nesten halvparten av alle såkalt signifikante funn egentlig er spuriøse, altså rent tilfeldige og uekte sammenhenger.

Perverse insentiver og vedvarende svakhet

Ettersom vi vet at lav statistisk styrke øker risikoen både for å gå glipp av reelle effekter og for å «finne» spuriøse effekter, og gitt at Cohen allerede tidlig på 1960-tallet dokumenterte et altfor lavt styrkenivå i den gjennomsnittlige psykologiforskningsstudien, skulle vi kanskje ha grunn til å forvente at forholdene er blitt bedre i dag.

Dessverre viser studier utført både på 1980-tallet (Sedlmeier & Gigerenzer, 1989) og ganske så nylig (Dumas-Mallet et al., 2017) at forholdene snarere er blitt verre. I en studie av studier inkludert i metaanalyser fra nevrovitenskapene holdt den typiske studien et skremmende lavt statistisk styrkenivå på rundt 21 % (Button et al., 2013).

Hvorfor blir det ikke bedre når vi vet så godt hvor lett det er å trekke feil konklusjoner fra en statistisk test med lav styrke? Cohen (1992) selv trodde det hadde å gjøre med at psykologer generelt er for lite opptatt av effektstørrelser. Radarparet Tversky og Kahneman (1971) har dokumentert at også noenlunde statistisk skolerte forskere undervurderer hvor store utvalg bør være og overvurderer hvor representative utvalg er, og gir oss dermed en annen mulig forklaring.

En tredje mulighet er etter min mening den som er aller mest interessant. I 2005 fremførte legen og statistikeren John P. A. Ioannidis (2005) en nå berømt forklaring på «hvorfor de fleste publiserte forskningsresultater er usanne» (min oversettelse). Den betingede alfasannsynligheten er helt sentral i denne forklaringen.

Ioannidis og andre forskere (Button et al., 2013; Higginson & Munafó, 2016; Vankov, Bowers & Munafò, 2014) peker også på et par andre forhold som er spesielt egnet til å hjelpe oss med å forstå hvorfor sikker kunnskap fra over et halvt århundre tilbake ikke fører til bedre forskningspraksis:

1. Det er større sannsynlighet for å få publisert et forskningsarbeid som har iøynefallende (altså overraskende, dvs. med lav P_H1 og høy P_H0) og statistisk signifikante resultater.
2. Forskeres karrierer bygger på antall publiserte arbeider og graden av oppmerksomhet disse arbeidene får.

Punkt 1 og 2 vil sammen utgjøre insentiver for å drive forskning på en slik måte at det øker sannsynligheten for å «finne» iøynefallende effekter. Slik praksis kan f.eks. innebære å gjennomføre mange små, utforskende studier hvor det gjennomføres mange statistiske tester, men hvor kun de pene, interessante og statistisk signifikante resultatene blir publisert. Slike mindre heldige forskningspraksiser forsterker problemene med lav statistisk styrke og øker sannsynligheten ytterligere for at et gitt «funn» ikke representerer en reell effekt.

Dette ser unektelig ganske mørkt ut. Og selv om det finnes øyer av håp, med pålitelige funn tuftet på store, gjentatte studier, så utgjør studier med tilstrekkelig statistisk styrke et lite mindretall både i medisin, psykologi og nevrovitenskap. Dette til tross for at etiske komiteer og forskningsfinansiører, mye takket være Cohens arbeider, nå ofte krever en styrkeanalyse før de godkjenner eller bevilger midler til en studie.

For den jevne konsumenten av psykologisk forskning er vel moralen kanskje denne: Vent med å tenke på noe som helst som et funn inntil resultater fra flere store (sterke) studier peker i samme retning.

Kilder

Button, K. S., Ioannidis, J. P. A., Mokrysz, C., Nosek, B. A., Flint, J., Robinson, E. S. J. & Munafò, M. R. (2013). Power failure: Why small sample size undermines the reliability of neuroscience. Nature Reviews Neuroscience, 14, 365. doi:10.1038/nrn3475

Cohen, J. (1962). The statistical power of abnormal-social psychological research: A review. Journal of Abnormal and Social Psychology, 65, 145–153. doi:10.1037/h0031322

Cohen, J. (1992). A power primer. Psychological Bulletin, 112, 155–159. doi:10.1037/0033-2909.112.1.155

Dumas-Mallet, E., Button, K. S., Boraud, T., Gonon, F. & Munafò, M. R. (2017). Low statistical power in biomedical science: A review of three human research domains. Royal Society Open Science, 4, 1–11. doi:10.1098/rsos.160254

Higginson, A. D. & Munafò, M. R. (2016). Current incentives for scientists lead to underpowered studies with erroneous conclusions. PLoS Biology, 14, 1–14. doi:10.1371/journal.pbio.2000995

Ioannidis, J. P. A. (2005). Why most published research findings are false. PLOS Medicine, 2, 1–6. doi:10.1371/journal.pmed.0020124

Kraemer, H. C. (2013). Statistical power: Issues and proper applications. I J. S. Comer & P. C. Kendall (red.), The Oxford handbook of research strategies for clinical psychology. Oxford: Oxford University Press. doi:10.1093/oxfordhb/9780199793549.013.0012

Overall, J. E. (1969). Classical statistical hypotheses testing within the context of Bayesian theory. Psychological Bulletin, 71, 285–292. doi:10.1037/h0026860

Sedlmeier, P. & Gigerenzer, G. (1989). Do studies of statistical power have an effect on the power of studies? Psychological Bulletin, 105, 309–316. doi:10.1037/0033-2909.105.2.309

Tversky, A. & Kahneman, D. (1971). Belief in the law of small numbers. Psychological Bulletin, 76, 105–110. doi:10.1037/h0031322

Vankov, I., Bowers, J., & Munafò, M. R. (2014). On the persistence of low power in psychological science. The Quarterly Journal of Experimental Psychology, 67, 1037-1040. doi:10.1080/17470218.2014.885986

1. Statistisk signifikans og statistisk hypotesetesting har også vært behandlet i en tidligere utgave av denne spalten. [↩]
2. Standardavviket er et vanlig mål på variasjon i et sett målinger. Grovt sett er det synonymt med enkeltverdienes gjennomsnittlige avstand fra gjennomsnittet av verdiene. Mye brukte mål på effektstørrelser i gjennomsnittsforskjeller mellom grupper er basert på standardavviket. [↩]
3. Enkel opptelling av antallet signifikante og ikke-signifikante effekter (ofte nedsettende omtalt som «bean counting») er derfor ikke en god måte å oppsummere forskning på. Statistiske metoder for å slå sammen resultater fra mange studier, metaanalyser, gir et mer sannferdig bilde, blant annet fordi de avhjelper noen av de problemene som skyldes lav statistisk styrke i enkeltstudiene. [↩]
4. Dette tallet har jeg funnet på, men det er ikke sikkert det er så urimelig, all den tid vi sjelden hører om nye terapier som er merkbart mer effektive enn de eksisterende. [↩]